冒泡与快速排序的算法原理与性能对比
一 概述
在日常开发过程中,我们经常需要对各种类型的数据进行排序,例如将订单按照金额进行降序排列。快速排序算法的时间复杂度为O(nlogn),空间复杂度为O(n)而常见的冒泡、选择、插入排序算法它的平均时间复杂度为O(n2),时间复杂度表示算法运行的时间,因此快速排序算法又被成为最优的排序算法。接下来主要对比冒泡排序和快速排序进行介绍、并对比两者性能的差异。
二 算法实现原理
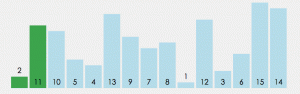
2.1.1 冒泡排序算法原理
-
从第一个元素开发遍历,比较相邻的元素。如果第一个比第二个大,就交换他们两个。
-
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
-
针对所有的元素重复以上的步骤,除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
2.1.2 代码实现
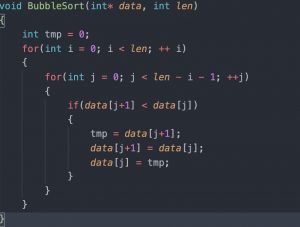
从代码可以看出这里使用了2层for循环,第一层for循环用于找出数组中第几大的数据,第二次for循环根据上层循环确定的数据和相邻的数据进行比较找出较大者,直到找到未被排序的数据为止。
2.2.1 快速排序算法原理
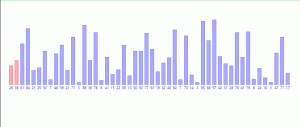
算法通过多次比较和交换来实现排序,其排序流程如下
-
首先设定一个分界值,通过该分界值将数组分成左右两部分。
-
将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值。
-
然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
-
重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
2.2.2 代码实现
下述代码每次就把第一个数据作为分界值,当然也可以通过随机数方式确定分界值,但会增加代码复杂度,期待大家来实现。

代码中虽然也有两层循环,但遍历关系却不是严格递进的,第2层循环可以改变第1层循环的判断条件,跳出循环后将界值放到low(界值在数组排序后的合理为止)。最后再对界值左边和右边的数据进行单独排序。
三 排序算法对比性能压测
通过随机生成10万个数据,分别用冒泡和快速排序算法对数据进行排序,分别计算出2种算法的耗时情况,得到时间复杂度对比。
![]()
从测试结果来看,对10万个数据进行排序冒泡排序需要24.86s快速排序只需要不到1s的时间,所以对海量数据进行排序时建议选择快速排序这种时间复杂度只需要nlog(n)的排序算法。
四 总结
-
从算法复杂性上来看,冒泡排序可以从生活中找到场景,实现逻辑相对简单、快速排序由于涉及到每趟都要更新分界值在理解上有一定的复杂度。
-
从算法时间复杂度的角度来看,在对大规模数据进行排序的时候快速排序的优势很明显,时间消耗相差2000倍,这也是STL里面sort函数使用快速排序的原因。
-
在快速排序里面由于选择分界值方法的不同,这就导致在极端条件下快速排序不够稳定可能会退化为冒泡排序,优先推荐使用三值取中法来选择分界值。相对而言,冒泡排序就非常的稳定。